Wind power calculator

This wind power calculator calculates the power output of a wind turbine, where it takes into account the air density ( $ρ$ ), rotor area ( $A$ ), wind speed ( $v$ ), and power coefficient ( $C_p$ ).

Air density (kg/m³):

Standard air density at sea level is 1.225 kg/m³

Wind speed (m/s):

Enter the wind speed in meters per second

Blade radius (m):

Enter the radius of the wind turbine blade (rotor area will be calculated as πr²)

Power coefficient (Cp):

Maximum theoretical efficiency is 0.59 (Betz's limit)

Wind power: 0 watts (0 MW)

Related calculators:

Wind chill Heat index Dew point Cloud base Temperature conversions

What is a wind turbine?

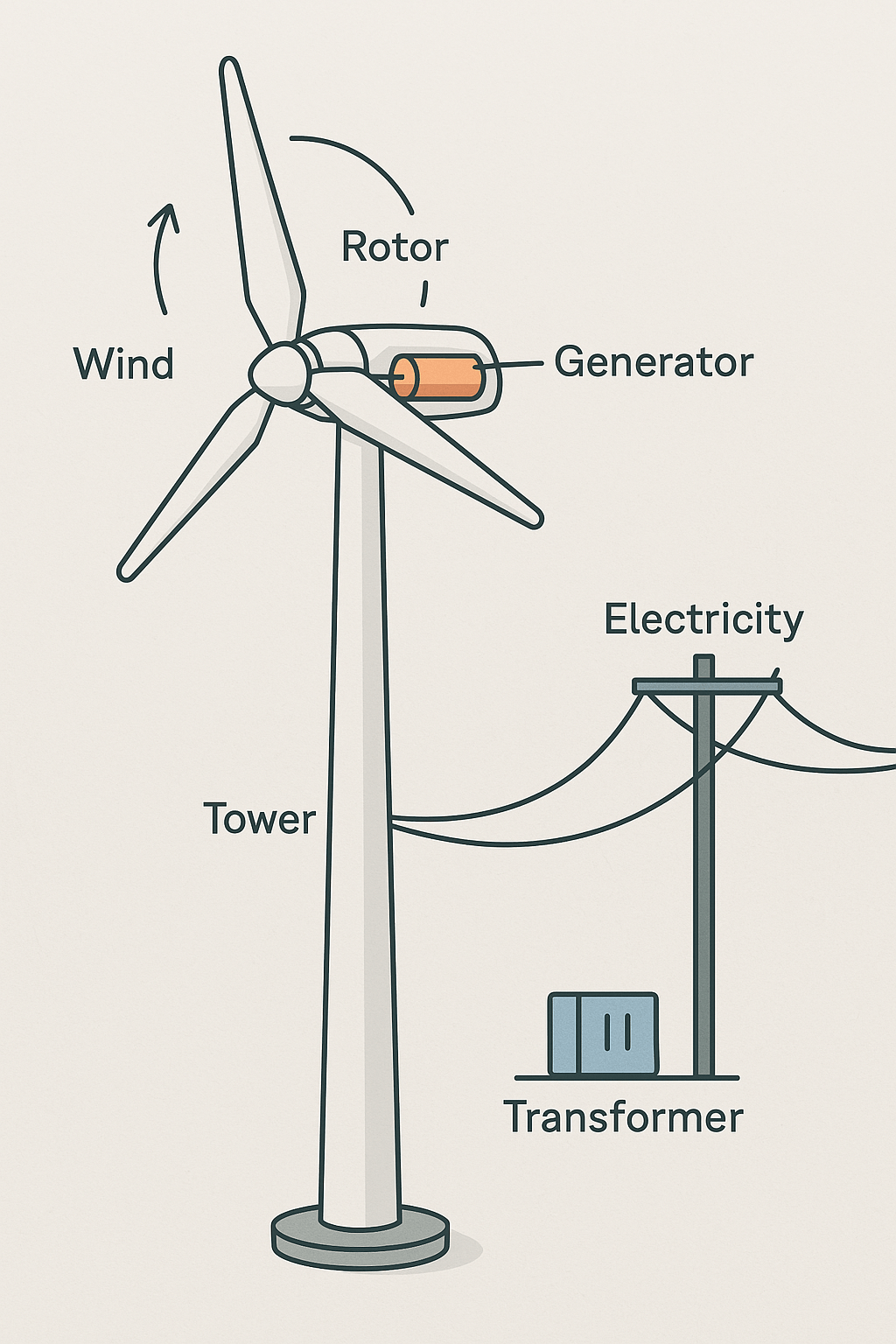
A wind turbine is a device that converts the kinetic energy of the wind into mechanical energy or electricity. It consists of several key components, including blades, a rotor, a generator, and a tower.

How it works:

Wind blows over the blades – The turbine’s blades capture wind energy and begin to rotate.
Rotor spins – The rotating blades turn the rotor, which is connected to a shaft.
Generator produces electricity – The shaft is connected to a generator, which converts mechanical energy into electrical energy.
Electricity is transmitted – The generated electricity is sent to a transformer and then distributed through power lines.

Types of wind turbines:

Horizontal-axis wind turbines (HAWTs)
- Most common type
- Large three-blade design
- Efficient for large-scale power generation
Vertical-axis wind turbines (VAWTs)
- Blades rotate around a vertical axis
- Can capture wind from any direction
- Used for smaller applications

What is wind power?

Wind power is the process of converting kinetic energy from the wind into mechanical or electrical energy using wind turbines. The movement of air due to temperature and pressure differences in the atmosphere generates wind, which can be harnessed for electricity generation.

Formula for wind power

The power extracted from the wind by a turbine is given by the following formula:

P = \frac{1}{2} \rho A V^3 C_p

where:

$P$ = Power output (watts)
$\rho$ = Air density ( $\text{kg/m}^3$ ) (typically around 1.225 kg/m³ at sea level)
$A$ = Rotor (swept) area of the turbine blades ( $\text{m}^2$ ) ( $A = \pi r^2$ , where $r$ is the blade length)
$V$ = Wind speed ( $\text{m/s}$ )
$C_p$ = Power coefficient (a measure of efficiency, typically $C_p \leq 0.59$ due to Betz’s limit)

The formula shows that wind power is highly dependent on wind speed ( $V^3$ ), meaning that small increases in wind speed result in much higher power output.

Example:

Given data:

Air density: $\rho = 1.225 \, \text{kg/m}^3$
Blade radius: $r=40m$
Wind speed: $V = 10 \, \text{m/s}$
Power coefficient: $C_p = 0.45$

Step 1: Calculate rotor (swept) area

A = \pi r^2 = \pi (40)^2 = 5026.55 \, \text{m}^2

Step 2: Calculate wind power

P = \frac{1}{2} \rho A V^3 C_p

P=\frac{1}{2}​(1.225)(5026.55)(10)^3(0.45)

P=1,385,442.84W=1,385.44kW\approx1.39MW

So, the wind turbine produces approximately 1.39 megawatts (MW) of power.