Quadratic formula solver

This quadratic formula solver helps solve equations in the form ax² + bx + c = 0. By applying the quadratic formula, the calculator quickly finds real or complex solutions and explains the nature of the roots using the discriminant.

Related calculators:

What is a quadratic equation?

A quadratic equation is a second-degree algebraic equation in which the highest power of the variable is 2. It is commonly written in the standard form:

ax² + bx + c = 0

where:

• x is the variable,
• a, b, and c are real numbers called coefficients,
• and a ≠ 0 (if a were zero, the equation would become linear).

Quadratic equations appear frequently in mathematics, physics, engineering, economics, and many real-world problem-solving situations.

How quadratic equations are wolved

There are several methods for solving quadratic equations, depending on their structure:

• Factoring, when the expression can be broken into simpler binomials
• Completing the square, which rewrites the equation into a perfect square form
• Graphing, where solutions are found by identifying x-intercepts
• Using the quadratic formula, which works for all quadratic equations

Among these methods, the quadratic formula is the most reliable because it applies universally, even when factoring is difficult or impossible.

The quadratic formula

The solutions of the quadratic equation ax² + bx + c = 0 can be found using the quadratic formula:

The symbol ± indicates that there are usually two solutions, obtained by using both the plus and minus signs.

Understanding the discriminant

The expression under the square root,

b² − 4ac,

is called the discriminant. It determines the nature of the solutions:

• Positive discriminant (b² − 4ac > 0): two distinct real solutions
• Zero discriminant (b² − 4ac = 0): one real repeated solution
• Negative discriminant (b² − 4ac < 0): two complex (non-real) solutions

Understanding the discriminant helps predict the number and type of solutions before solving the equation.

What do the solutions represent?

The solutions of a quadratic equation are also called its roots or zeros. Graphically, these correspond to the points where the parabola defined by the equation crosses (or touches) the x-axis.

Depending on the context, quadratic solutions may represent:

• Time or position in motion problems
• Maximum or minimum values in optimization
• Break-even points in economic models
• Physical limits or boundaries in engineering applications

Relationship between the quadratic formula and the graph

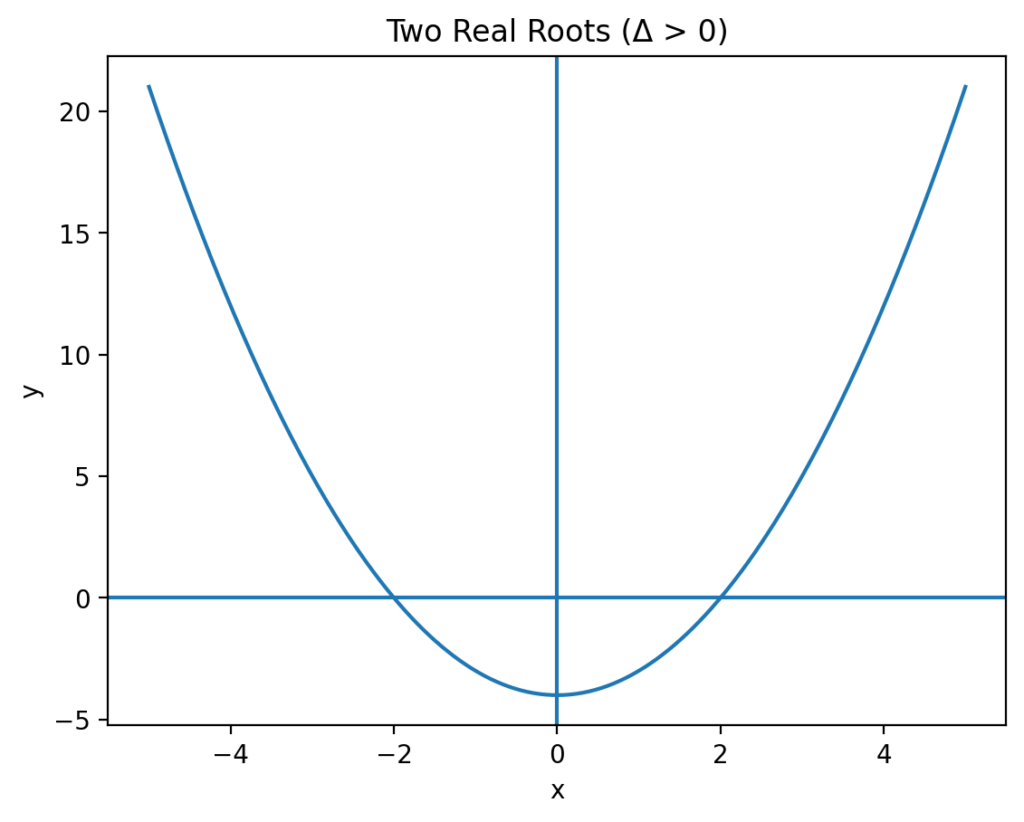
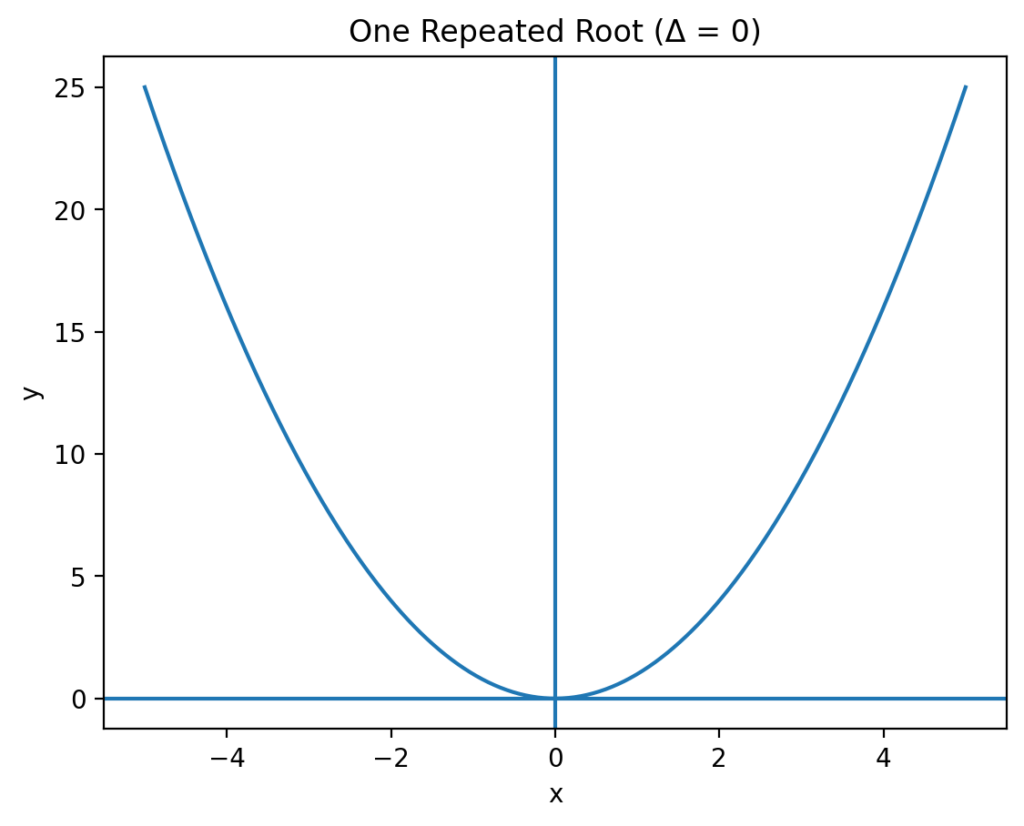
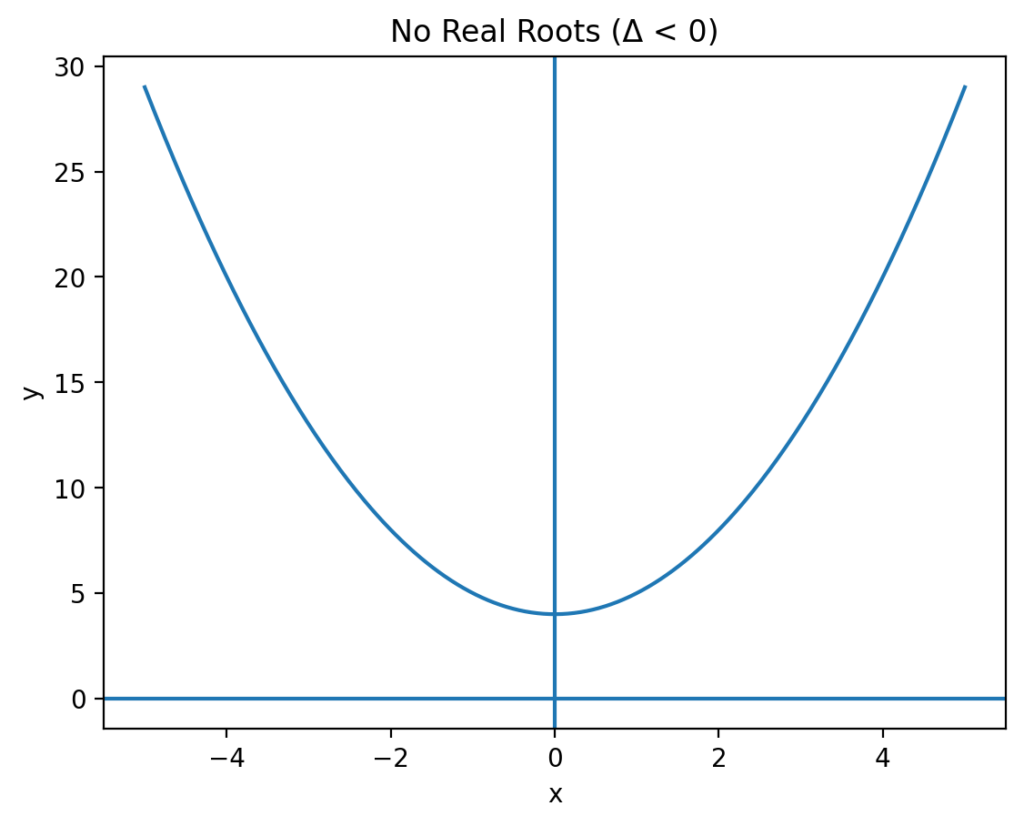
Every quadratic equation represents a parabola when graphed on a coordinate plane. The solutions obtained from the quadratic formula correspond directly to key features of this graph.

The values of x found using the quadratic formula are called the roots (or zeros) of the equation. Graphically, these are the points where the parabola intersects or touches the x-axis.

The discriminant plays an important role in determining how the graph behaves:

• If the discriminant is positive (see the first graph below), the parabola crosses the x-axis at two distinct points, resulting in two real solutions.
• If the discriminant is zero (see the second graph below), the parabola touches the x-axis at exactly one point, producing one repeated real solution.
• If the discriminant is negative (see the third graph below), the parabola does not intersect the x-axis, and the equation has no real solutions.

In addition, the coefficient a determines the shape and direction of the graph. When a > 0, the parabola opens upward, and when a < 0, it opens downward. The roots found using the quadratic formula help identify where this curve meets the x-axis, providing a clear connection between algebraic solutions and their graphical interpretation.